생각하는 감쟈
[Python] 4-4) 머신러닝 - 그래디언트,커널 본문

✔4DAY
그래디언트 부스팅 회귀 트리
커널 서서포트 벡터 머신
커널기법
출처 입력
그래디언트 부스팅 회귀 트리
- 여러 개의 결정트리를 묶어 강력한 모델을 만드는 앙상블 기법 중 하나
- 이름은 회귀히지만 회귀와 분류에 모두 사용 가능
- 랜덤포레스트와 달라 이전 트리의 오차를 보완하는 방식
- 순차적으로 트리 생성
- 무작이성이 없음
- 강력한 사전 가지치기를 하용하는 방식
- 보통 하나에서 다섯 정도의 깊지 않은 트리 사용
- 빠른 예측과 적은 메모리 사용량
높은 정확도의 그래디언트 부스팅 트리
- 머신러닝 경연 대회 다수 우승
- 업계에서도 널리 사용
- 매개변수 설정에 따라 높은 정확도 제공
- 랜덤 폴스트 보다 매개변수 설정에 조금 더 민감한 편
- 중요한 매개 변수
- 앙상블 방식의 사전 가지치기, 트리 개수
- 이전트리의 오차 보정치 제어값
- learning_rate : 학습률
- 학습률이 크면 트리를 강하게 보정하여 복잡한 모델 생성
- 앙상블에 추가할 트래 갯수
- n_estimeators : 트리 개수
- 값을 높이면 앙상블에 트리가 더 많이 추가
- 모델의 복잡도 증가
- 훈현 세트에서 실수를 바로 잡을 기회 증가
from sklearn.ensemble import GradientBoostingClassifier
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, random_state=0)
gbrt = GradientBoostingClassifier(random_state=0)
gbrt.fit(X_train, y_train)
print("훈련 세트 정확도: {:.3f}".format(gbrt.score(X_train, y_train)))
print("테스트 세트 정확도: {:.3f}".format(gbrt.score(X_test, y_test)))
훈련 세트 정확도: 1.000
테스트 세트 정확도: 0.958gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)
print("훈련 세트 정확도: {:.3f}".format(gbrt.score(X_train, y_train)))
print("테스트 세트 정확도: {:.3f}".format(gbrt.score(X_test, y_test)))
훈련 세트 정확도: 0.991
테스트 세트 정확도: 0.972gbrt = GradientBoostingClassifier(random_state=0, learning_rate=0.01)
gbrt.fit(X_train, y_train)
print("훈련 세트 정확도: {:.3f}".format(gbrt.score(X_train, y_train)))
print("테스트 세트 정확도: {:.3f}".format(gbrt.score(X_test, y_test)))
훈련 세트 정확도: 0.988
테스트 세트 정확도: 0.965
gbrt = GradientBoostingClassifier(random_state=0, max_depth=1)
gbrt.fit(X_train, y_train)
plot_feature_importances_cancer(gbrt
대규모 머신러닝 문제
- 대규모 머신러닝 문제 해결 시 발생되는 성능 문제
- 그래디언트 부스팅을 적용하는 것이 유리
- xgboost 패키지와 파이썬 인터페이스 사용하는 것이 좋음
- scikit-learn의 그래디언트 부스팅 보다 빠름
- 튜닝하기도 편함
장점
- 지도학습에서 가장 강력함
- 가장 널리 사용하는 모델 중의 하나
- 특성의 스케일 조정이 필요
- 이진 특성이 연솓적인 특성에도 잘 동작
단점
- 매개변수를 잘 조정해야 한다는 것
- 긴 훈련 시간
- 트리 기반 모델을 사용
- 희소한 고차원 데이터에는 부적합
중요한 매개변수
- n_estimators
- 트리의 개수 지정
- 너무 클 모델이 복잡해지고 과대적합 가능성
- learning_rate
- 이전 트리의 오차 보정 강도 조절(학습률)
- 두 개의 매개변수는 깊이 연관선
- learning_rate를 낮추면, 복잡도 유지를 위해 트리를 추가해야함
일반적인 관례
- 가용한 시간과 메모리 한도에서 n_setimatores 부터 설정
- 이후 적절한 learning_rate 설정
커널서포트벡터 머신
SVM
- 입력데이터에서 단순한 초평면으로 정의되지 않는 더 복잡한 모델을 만들 수 있도록 확장한 지도 학습 모델
- 분류와 회귀에 모두 사용 가능
- SVR를 사용하는 회귀 문제에도 같은 개념을 적용 가능
- 수학적으로 매우 복잡한 알고리즘
선형모델과 비선형 특성
- 직선과 초평면의 유연하지 못한 문제
- 저차원 데이터셋에서는 선형 모델이 매우 제한적
- 선형 모델을 유연하게 만드는 방법
- 특성끼리 곱하거나, 특성을 거듭제곱식으로 새로운 특성을 추가하는 방식
X, y = make_blobs(centers=4, random_state=8)
y = y % 2
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
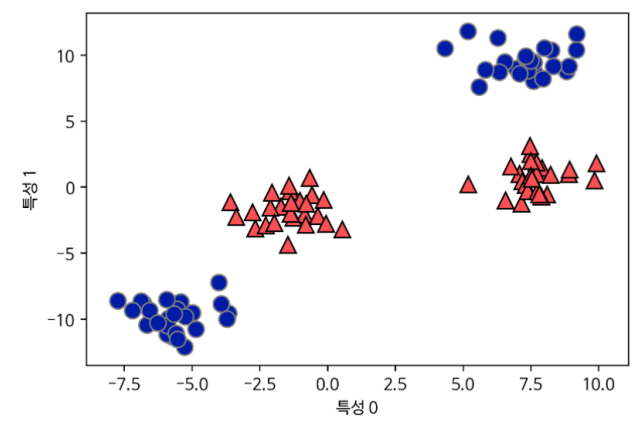
분류를 위한 선형 모델의 한계
- 직선으로만 데이터 포인트를 나누는 방식
from sklearn.svm import LinearSVC
linear_svm = LinearSVC().fit(X, y)
mglearn.plots.plot_2d_separator(linear_svm, X)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
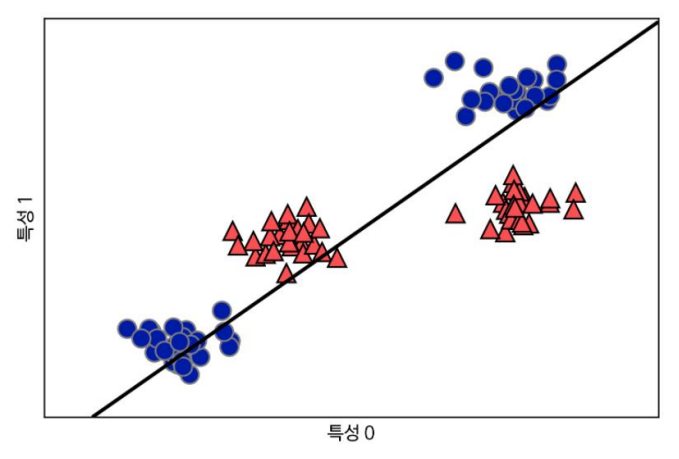
새로운 특성을 추가해 입력 특성 확장
- 두번째 특성을 제곱(**) 하여 새로운 특성으로 추가
- 2차원(특성0, 특성1) > 3차원(특성0,특성1,특성1**2)
X_new = np.hstack([X, X[:, 1:] ** 2])
from mpl_toolkits.mplot3d import Axes3D, axes3d
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)
mask = y == 0
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
cmap=mglearn.cm2, s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r',
marker='^', cmap=mglearn.cm2, s=60, edgecolor='k')
ax.set_xlabel("특성0")
ax.set_ylabel("특성1")
ax.set_zlabel("특성1 ** 2")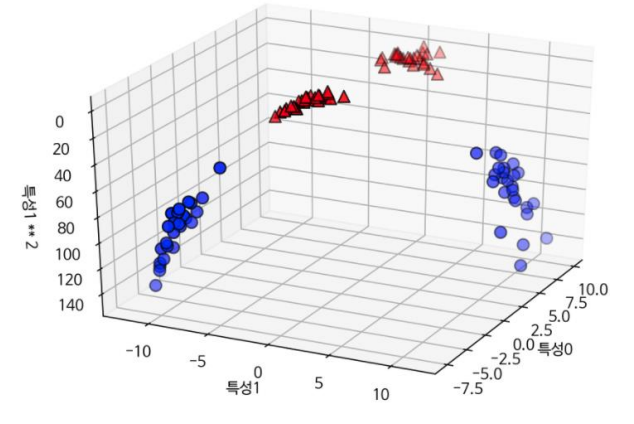
3차원 산점도 출력
- 3차원으로 확장된 데이터셋
- 선현 모델과 3차원 공간의 평면을 사용해 두 클래스를 구분 가능
linear_svm_3d = LinearSVC().fit(X_new, y)
coef, intercept = linear_svm_3d.coef_.ravel(), linear_svm_3d.intercept_
figure = plt.figure()
ax = Axes3D(figure, elev=-152, azim=-26)
xx = np.linspace(X_new[:, 0].min() - 2, X_new[:, 0].max() + 2, 50)
yy = np.linspace(X_new[:, 1].min() - 2, X_new[:, 1].max() + 2, 50)
XX, YY = np.meshgrid(xx, yy)
ZZ = (coef[0] * XX + coef[1] * YY + intercept) / -coef[2]
ax.plot_surface(XX, YY, ZZ, rstride=8, cstride=8, alpha=0.3)
ax.scatter(X_new[mask, 0], X_new[mask, 1], X_new[mask, 2], c='b',
cmap=mglearn.cm2, s=60, edgecolor='k')
ax.scatter(X_new[~mask, 0], X_new[~mask, 1], X_new[~mask, 2], c='r',
marker='^', cmap=mglearn.cm2, s=60, edgecolor='k')
ax.set_xlabel("특성0")
ax.set_ylabel("특성1")
ax.set_zlabel("특성1 ** 2")
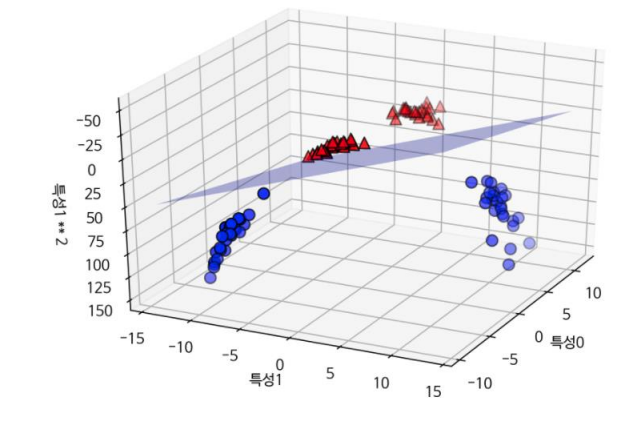
원래 특성으로 투영해 보면 더 이상 선형이 아님
- 직선 보다 타원에 가까운 모습의 모델
ZZ = YY ** 2
dec = linear_svm_3d.decision_function(np.c_[XX.ravel(), YY.ravel(),
ZZ.ravel()])
plt.contourf(XX, YY, dec.reshape(XX.shape), levels=[dec.min(), 0, dec.max()],
cmap=mglearn.cm2, alpha=0.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
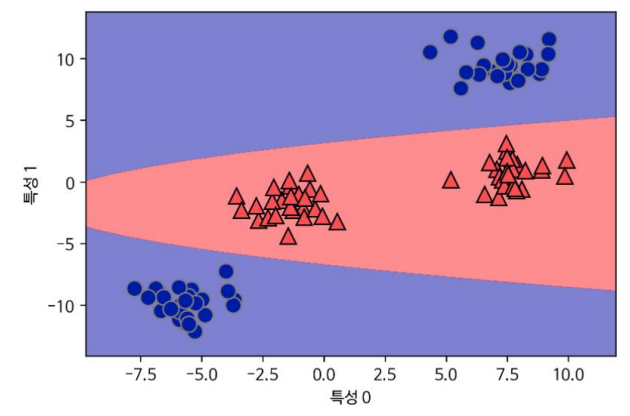
- 데이터 셋에 비선형 특성을 추가하여 강력한 선형 모델 생성 가능
- 어떤 특성을 추가해야할지 파악하기 어려운 문제
- 특성을 지나치게 주가할 경우 연산 비용 증가 문제
커널기법
- 수학 연산으로 새 특증을 만들지 않고 고차원에서 분류기를 학습 시키는 방법
- 실제 데이터를 확장하지 않고 확장된 특성에 대한 데이터 포인트들의 거리 게산
- 포인트들의 거리 : 스칼라 곱
서포트 백터 머신에서 데이터를 고차원 공안에 매핑 방법 2가지
- 다항식 커널
- 원래 특성의 가능한 조합을 지정된 차수까지 모두 계산하는 방법
- RBF 커널
- 가우시안 커널로도 가능
- 차원이 무한한 특성 공간에 매핑하는 방법
- 모든 차수의 모든 다항식을 고려하는 방식
- 고차항이 될 수록 해당 특성의 중요도는 떨어짐
SVM 이해하기
- SVM의 학습
- 각 훈련 데이터 포인들의 중요도를 파악해 가는 과정
- 두 클래스 사이의 결정 경계 생성 시 중요도
- 각 훈련 데이터 포인들의 중요도를 파악해 가는 과정
- 서포트 벡터
- 일반적으로 훈련데이터의 일부만 결정경계 생성에 영향
- 두 클래스 사이의 경계에 위치한 데이터 포인트들
- 서포트 벡터 머신아란 이름의 유래
- 새로운 데이터 포안터에 대해 예측하기
- 각 서포트 백터와의 거리를 측정
- 분류 결정은 서포트 백터싸지의 거리에 기반
- 서포트 백터의 중요도는 훈련 과정에서 학습
- svc 객체의 dual_coef_ 속성에 저장
- 데이터 포인트 사이의 거리
- 사우시안 커널에 의해 계산

-
- x1, x2 : 데이터 포인트
- || x1 - x2 || : 유클리디안 거리
- y ( 감마, gamma) : 가우시안 커널의 폭을 제어
forge 데이터셋에 svm을 학습시켜 그래프 그리기
- 2개의 클래스를 가진 2차원 데이터셋에 서프터 백터 머신 학습 시키기
from sklearn.svm import SVC
X, y = mglearn.tools.make_handcrafted_dataset()
svm = SVC(kernel='rbf', C=10, gamma=0.1).fit(X, y)
mglearn.plots.plot_2d_separator(svm, X, eps=.5)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
sv = svm.support_vectors_
sv_labels = svm.dual_coef_.ravel() > 0
mglearn.discrete_scatter(sv[:, 0], sv[:, 1], sv_labels, s=15,
markeredgewidth=3)
plt.xlabel("특성 0")
plt.ylabel("특성 1")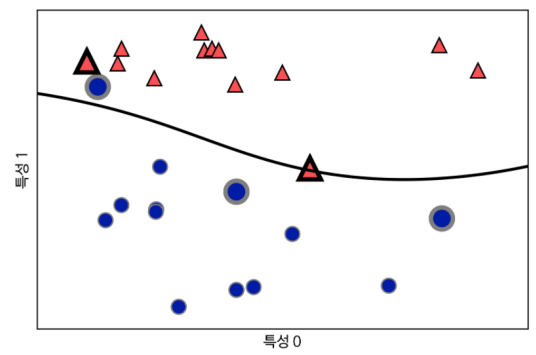
RBF 커널을 사용한 SVM으로 만든 결정경계와 서포트 벡터
- 결정 경계는 검은 실선
- 서포트 벡터는 굵은 테두리
- SVM은 매우 부드러운 곡선 경계를 생성
- 두 매개변수 (C, gamma) 사용
gamma 매개변수
- 가우시안 커널 폭의 역수
- 하나의 훈련 샘플이 미치는 영향의 범위 결정
- 작은 값 : 넓은 영역
- 큰 값 : 좁은 영역
- 카우시안 커널의 반경이 클 수록 훈련 샘플의 영향 범위도 증가
- 가우시안 커널의 반경이 클 수록 훈련 샘플의 영향 범위도 증가
C 매개변수
- 선형 모델에서 사용한 것과 비슷한 규제 매개변수
- 각 포인트의 중요도 (dual_coef_ 값)를 제한
매개변수 값을 변화시켜 보기
fig, axes = plt.subplots(3, 3, figsize=(15, 10))
for ax, C in zip(axes, [-1, 0, 3]):
for a, gamma in zip(ax, range(-1, 2)):
mglearn.plots.plot_svm(log_C=C, log_gamma=gamma, ax=a)
axes[0, 0].legend(["클래스 0", "클래스 1", "클래스 0 서포트 벡터", "클래스 1 서
포트 벡터"], ncol=4, loc=(.9, 1.2))
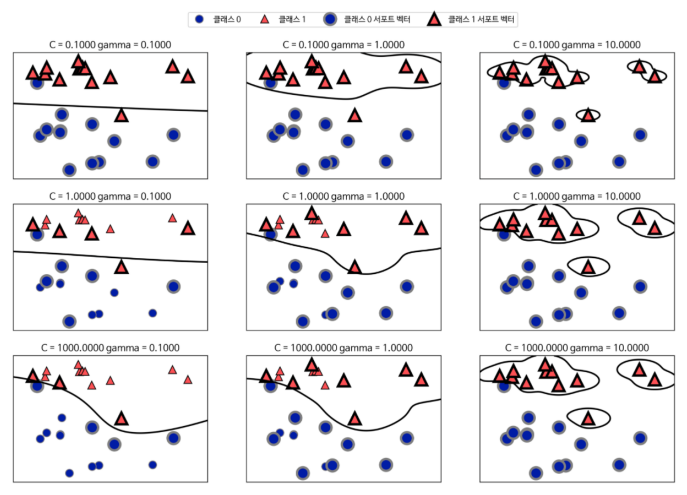
실험 결과 분석
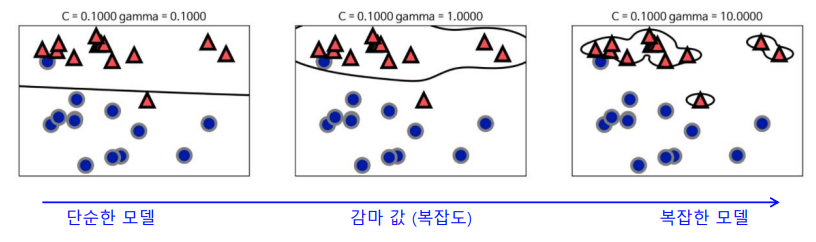
왼쪽에서 오른쪽으로 가면서 gamma 값 증가
- 작은 gamma값
- 가우시안 컨널 반경을 증가 시켜 가까운 포인트 사용
- 왼쪽 그림은 매우 부드럽고 오른쪽은 각 포인트에 민감해짐
- 작은 gamma 값이 결정 경계를 부드럽게해 보델 복잡도를 낮춤
- 큰 gamma 값
- 더 복잡한 모델 생성
위에서 아래로 가면서 C값 증가
- 작은 C값 (위쪽) : 높은 제약
- 제약이 높은 모델 생성
- 각 데이터 포인터의 영향력이 작아짐
- 선형에 가까운 결정 경계 생성
- 잘못 분류된 데이터 포인트가 경계에 거의 영향을 주지 않음
- 큰 C값(아래쪽) : 낮은 제약
- 포인트들이 모델에 큰 영향을 끼침
- 결정 경계를 휘어서 정확하게 분류
유방암 데이터셋에 적용
cancer.data, cancer.target, random_state=0)
svc = SVC()
svc.fit(X_train, y_train)
print("훈련 세트 정확도: {:.2f}".format(svc.score(X_train, y_train)))
print("테스트 세트 정확도: {:.2f}".format(svc.score(X_test, y_test)))
훈련 세트 정확도: 1.00
테스트 세트 정확도: 0.6SVM은 잘 잘동하는 편이지만 매개변수 설정과 데이터 스케일이 매우 민감
- 입력 특성의 범위가 비슷해야 함
각 특성의 최소값과 최대값을 로그스케일로 표시하기
plt.boxplot(X_train, manage_xticks=False)
plt.yscale("symlog")
plt.xlabel("특성 목록")
plt.ylabel("특성 크기")
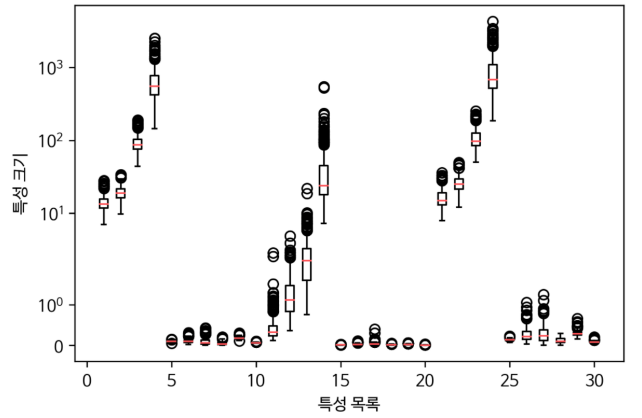
TEXT(0,0.5,'특성크기')자리수엣 큰 차이를 보이는 데이터 특성
- Y축은 로그 스케일
- 데이터 특성의 크기가 1000배가지 차이가 있어 커널 SVM에서는 문제 발생 가능
특성 값의 범위가 비슷해지도록 조정하기
- 커널 SVM에서는모든 특성 값을 0과 1사이로 맞추는 방법 사용
- MinMaxScaler 전처리 ㅂ메서드를 이용해 맞출수 있으나. 직접 구현해보기
커널 서포트 벡트 머신의 장단점
- 강력한 모델이며, 다양힌 데이터셋에서 잘 작동
- 데이터의 특성이 몇개 안되더라도 복잡한 결정 경계를 잘 만들 수 있음
- 저차원과 고차원의 데이터(특성이 적을 떄와 많을 때)에 모두 잘 작동
- 샘플이 많을 때에는 잘 맞지 않음
- 10,000개의 샴플 정조에서 SVM 모델이 잘 작동
- 100,000개 이상의 데이터셋에서는 속도와 메모리의 한계
- 데이터 전처리와 매개변수 설정의 어려움
- 일반적으로 전처리가 필요없는 트리 기반 모델을 주로 사용
- 분석이 어려움
- 예측이 어떨게 결정되었는지 이해하기 어려움
- 비전문가에게 모델을 설명하기 난해함
- 모든 특성이 비슷한 단위이고, 스케일이 비슷하면 SVM이 적합함
딥러닝과 신경망
딥러닝
- 신경망이라고 알려진 알고리즘들은 최근 딥러닝이란 이름으로 주목
- 많은 머신러닝 응용에서 매우 희망적인 성과
- 특정 분야에 정교하게 적용되어 있는 경우가 많음
다층 퍼셉트론(MLP)
- 복잡한 딥러닝 알고리즘의 출발점
- 비교적 간단하게 분류와 회귀에 사용 가능
- 피드포워드 신경망, 또는 그냥 신경망이라고 부름
MLP
- 여러 단계를 거쳐 결정을 만들어내는 선형 모델의 일반화된 모습
- 선형 회귀 모델의 예측 공식
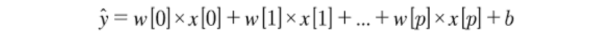
사진 설명을 입력하세요.
- 선형 회귀 모델의 예측 공식을 그래프로 표시하기
로지스틱 회귀 그래프
- 입력 특성과 예측은 노드로 표시
- 왼쪽 노드는 입력 특성
- 오른쪽 노드는 입력의 가중치를 합한 출력
- 학습된 계수는 노드 사이의 연결로 표시
MLP
- 가중치의 합을 만드는 과정이 여러번 반복
- 먼전 중간 단계를 구성하는 은딕 유닛을 계산
- 최종 결과를 산출하기 위해 다시 가중치의 합을 계산
MLP의 은닉층
- MLP은 많은 계수를 학습해야 함
- 계수는 각 입력고 은닉층의 은닉 유닛 사이, 각 은닉 유닛과 출력 사이마다 존재
- 여러개의 가중치 합을 계산하는 것
- 수학적으로 보면 하나의 가중치 합을 계싼하는 것과 동일
- 선형 모델보다 걍력하게 만들기 위한 기법
- 각 은닉 유닛의 가중치 합을 계산
- 비선형 함수인 렐루나 하이퍼볼릭 탄젠트 적용
- 이 함수 결과의 가중치 합을 계사나여 출려
비선형 함수를 이용해 훨씬 더 복잡한 함수 학습 가능
- 렐루 함수는 0이하를 잘라버림
- hanh함수는 낮은 입력값에 대해서는-1로 수렴, 큰 입력값은 +1로 수렴
line = np.linspace(-3, 3, 100)
plt.plot(line, np.tanh(line), label="tanh")
plt.plot(line, np.maximum(line, 0), linestyle='--', label="relu")
plt.legend(loc="best")
plt.xlabel("x")
plt.ylabel("relu(x), tanh(x)")
사진 설명을 입력하세요.
은닉충 추가하기
- 많은 은닉층으로 구성된 대규모 신경망이 생기면서 딥러닝이라고 부르게 됨
mglearn.plots.plot_two_hidden_layer_graph()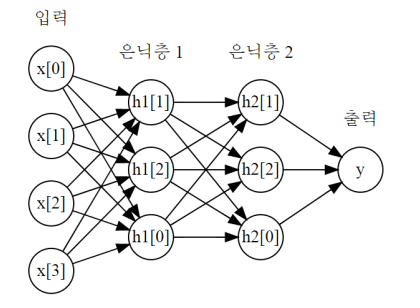
two_moons 데이터셋 활용
- 분류를 위한 다층 퍼셉트론(MLP)구현인 MLPClassifier 적용하기
from sklearn.neural_network import MLPClassifier
from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.25, random_state=3)
X_train, X_test, y_train, y_test = train_test_split(X, y, stratify=y,
random_state=42)
mlp = MLPClassifier(solver='lbfgs', random_state=0).fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
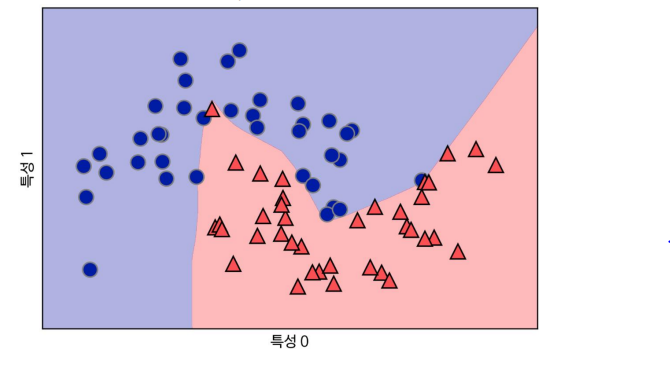
two_moons 데이터셋의 결정경계
- 은닉 유닛이 100개인 신경망으로 학습
- 매우 비선형적이지만,비교적 매끄러운 결정 경계 생성
- solver 매개변수, 최적화 알고리즘 지정
MLP
- 기본 값으로 은닉 유닛 100개 사용
- 작은 데이터셋에는 너무 큰 크기
- 은닉 유닛의 개수를 줄여도 좋은 결과를 얻을 수 있음
- 은닉 유닛의 개수를 줄이면 복잡도가 낮아지는 효과
mlp = MLPClassifier(solver='lbfgs', random_state=0,
hidden_layer_sizes=[10])
mlp.fit(X_train, y_train)
mglearn.plots.plot_2d_separator(mlp, X_train, fill=True, alpha=.3)
mglearn.discrete_scatter(X_train[:, 0], X_train[:, 1], y_train)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
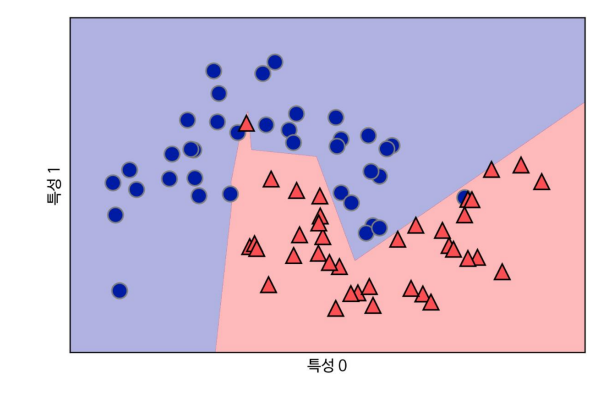
two_moons 데이터셋의 결정 경계
- 은닛 유닛이 10개인 신경망으로 학습하여, 이전 보다 날카로워진 모습
- 기본 비선형 함수는 ReLU 사용
- 은닉충이 하나이므로. 결정 경계를 만드는 함수는 직선 10개가 합쳐져서 구성됨

'Language > Python' 카테고리의 다른 글
| [Python] 5-2) 딥러닝 흐름2 (0) | 2023.06.10 |
|---|---|
| [Python] 5-1) 딥러닝 흐름 (0) | 2023.06.10 |
| [Python] 4-3) 머신러닝 - 결정트리.. (1) | 2023.04.13 |
| [Python] 4-2) 머신러닝 - 지도학습 알고리즘 (1) | 2023.04.13 |
| [Python] 4-1) 머신러닝 기초 (0) | 2023.04.06 |
