[Python] 4-2) 머신러닝 - 지도학습 알고리즘
19일차 (23.04.06)

✔ 2DAY
K-NN 알고리즘
K-NEIGHBORS REGRESSION 알고리즘
선형모델
릿지회귀
라쏘
분류용 선형모델
딥러닝 머신러닝 차이점
특징점을 사람이하느냐 스스로 하느냐 차이
k-최근접 이웃 회귀
mglearn.plots.plot_knn_regression(n_neighbors=1)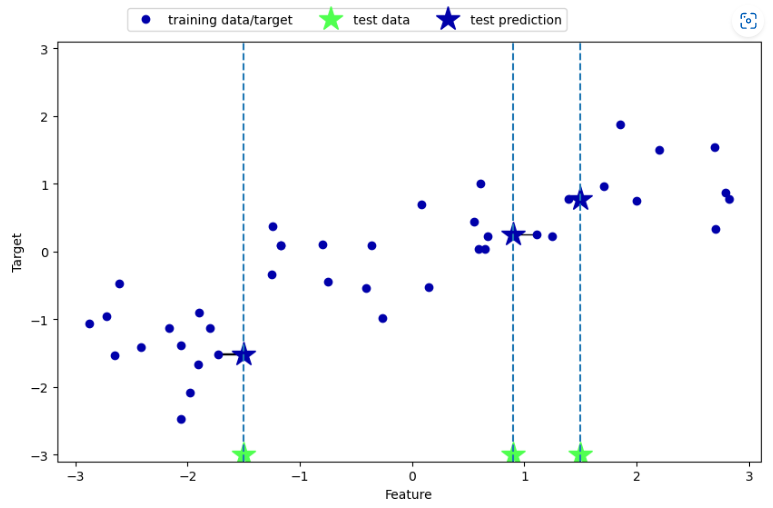
mglearn.plots.plot_knn_regression(n_neighbors=3)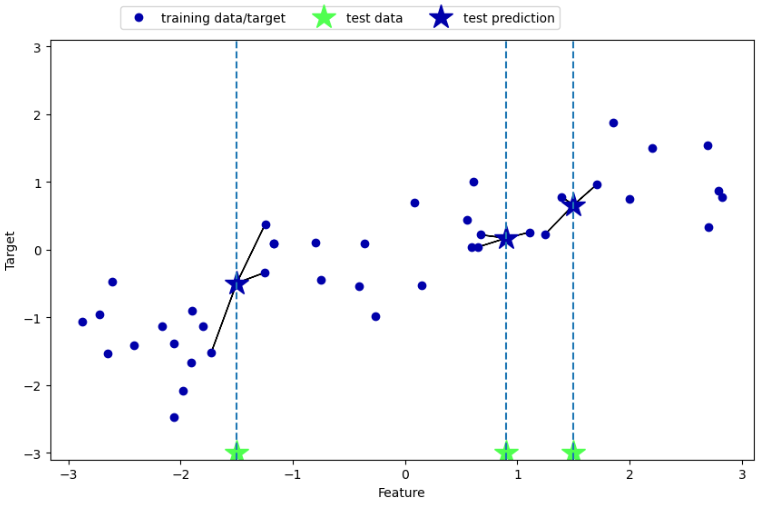
from sklearn.neighbors import KNeighborsRegressor
X,y = mglearn.datasets.make_wave(n_samples=40)
X_train, X_test,y_train,y_test = train_test_split(X,y,random_state=0)
reg = KNeighborsRegressor(n_neighbors=3)
reg.fit(X_train, y_train)print("테스트 세트 예측:\n", reg.predict(X_test))
print("테스트 세트 R^2: {:.2f}".format(reg.score(X_test, y_test)))테스트 세트 예측:
[-0.05396539 0.35686046 1.13671923 -1.89415682 -1.13881398 -1.63113382
0.35686046 0.91241374 -0.44680446 -1.13881398]
테스트 세트 R^2: 0.83K-NEIGHBORS REGRESSION 분석
fig,axes = plt.subplots(1,3,figsize=(15,4))
line = np.linspace(-3,3,1000).reshape(-1,1)
for n_neighbors, ax in zip([1,3,9], axes):
reg=KNeighborsRegressor(n_neighbors=n_neighbors)
reg.fit(X_train, y_train)
ax.plot(line, reg.predict(line))
ax.plot(X_train, y_train,'^',c=mglearn.cm2(0),markersize=8)
ax.plot(X_test, y_test,'v',c=mglearn.cm2(1),markersize=8)
ax.set_title(
"{} 이웃의 훈련 스코어: {:.2f} 테스트 스코어 : {:.2f}".format(
n_neighbors, reg.score(X_train, y_train),
reg.score(X_test,y_test)))
ax.set_xlabel("특성")
ax.set_ylabel("타깃")
axes[0].legend(["모델 예측","훈련데이터/타깃","테스트 데이터/타깃"],loc="best")
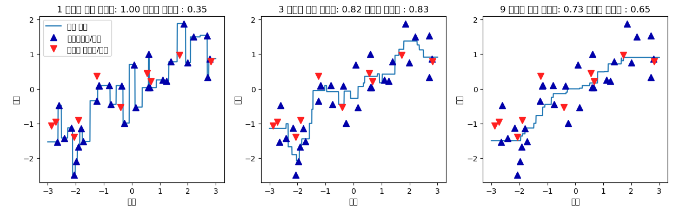
선형모델
- 최근 폭 넓게 연구되고 현재도 널리 쓰이는 모델
- 입력 특성에 대한 선형 함수를 만들어 에측을 수행하는 방식
회귀의 선형 모델의 일반적 예측 함수
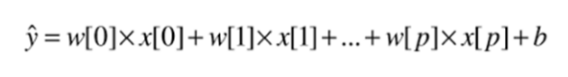
x[0] 부터 x[p]까지
- 하나의 데이터 포인드에 대한 특성을 나타냄
특성의 개수 : p+1
w,b : 모델의 학습할 파라미터
y : 모델이 만들어낸 예측값
특성이 하나인 데인터 값(위 식 단순화)
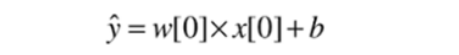
직선의 방정식
w[0] : 기울기
b는 y축과 만나는절편
특성이 많아지면 w는 각 특성에 해당하는 기울기를 모두 가짐
- 예측값은 입력 특성에 w의 각 가중치를 겁해서 더한 가중치의 합
- 가중치는 음수일 수 있음
mglearn.plots.plot_linear_regression_wave()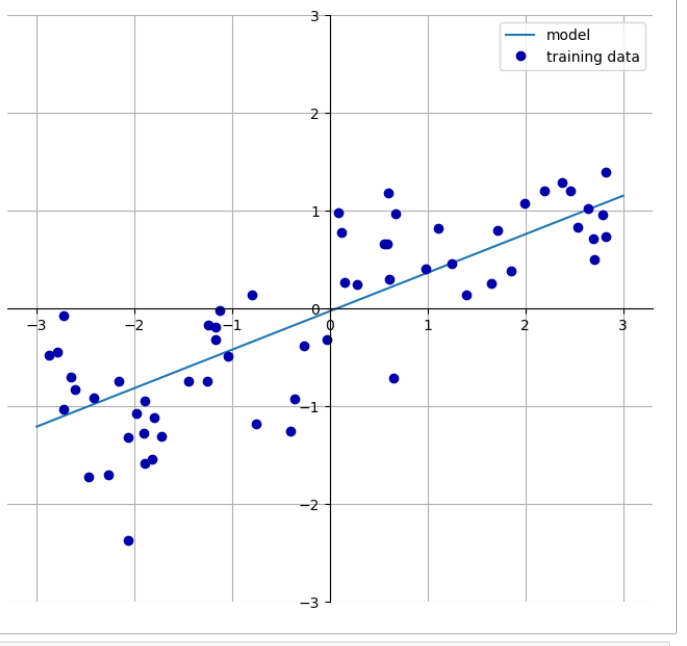
선형 모델(최소제곱법)
from sklearn.linear_model import LinearRegression
X,y = mglearn.datasets.make_wave(n_samples=60)
X_train, X_test,y_train,y_test = train_test_split(X,y,random_state=42)
lr=LinearRegression().fit(X_train,y_train)print("lr.coef_:", lr.coef_)
print("lr.intercept_:", lr.intercept_)lr.coef_: [0.39390555]
lr.intercept_: -0.031804343026759746print("훈련 세트 점수 :{:.2f}".format(lr.score(X_train, y_train)))
print("테스트 세트 점수 :{:.2f}".format(lr.score(X_test, y_test)))
훈련 세트 점수 :0.67
테스트 세트 점수 :0.66X,y = mglearn.datasets.load_extended_boston()
X_train, X_test,y_train,y_test = train_test_split(X,y,random_state=0)
lr=LinearRegression().fit(X_train,y_train)print("set:{:.2f}".format(lr.score(X_train,y_train)))
print("dataset:{:.2f}".format(lr.score(X_test,y_test)))set:0.95
dataset:0.61리지 회귀
릿지도 화귀를 위한 선형 모델
- 최소적합법에서 사용한 것과 같은 예측 함수를 사용
- 가중치의 선택
- 훈련 데이터를 잘 예측하기 위한 목적
- 추가 제약 조건을 만족 시키기 위한 목적
- L2규제
- 과대적합이 되지 않도록 모델을 강제로 제한
- 가중치의 절대값을 가능한 한 작게 만드는 것
- w의 모근 원소가 0에 가깝게 하기
- 모든 특성이 출력에 주는 영향을 최소화
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train,y_train)
print("set score :{:.2f}".format(ridge.score(X_train,y_train)))
print("test score :{:.2f}".format(ridge.score(X_test,y_test)))set score :0.89
test score :0.75ridge10=Ridge(alpha=10).fit(X_train, y_train)
print("set score :{:.2f}".format(ridge10.score(X_train,y_train)))
print("test score :{:.2f}".format(ridge10.score(X_test,y_test)))set score :0.79
test score :0.64ridge01=Ridge(alpha=0.1).fit(X_train, y_train)
print("set score :{:.2f}".format(ridge01.score(X_train,y_train)))
print("test score :{:.2f}".format(ridge01.score(X_test,y_test)))set score :0.93
test score :0.77plt.plot(ridge10.coef_,'^',label="Ridge alpha=10")
plt.plot(ridge.coef_,'s',label="Ridge alpha=1")
plt.plot(ridge01.coef_,'v',label="Ridge alpha=0.1")
plt.plot(lr.coef_,'o',label="LinearRegression")
plt.xlabel("계수목록")
plt.ylabel("계수크기")
xlims=plt.xlim()
plt.hlines(0,xlims[0],xlims[1])
plt.xlim(xlims)
plt.ylim(-25,25)
plt.legend()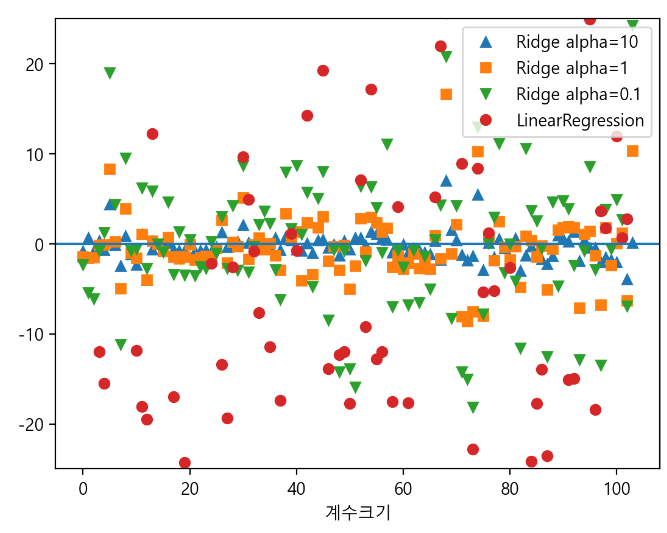
규제 효과의 이해
- alpha 값을 고정하고 훈련 데이터의 크기 조절
mglearn.plots.plot_ridge_n_samples()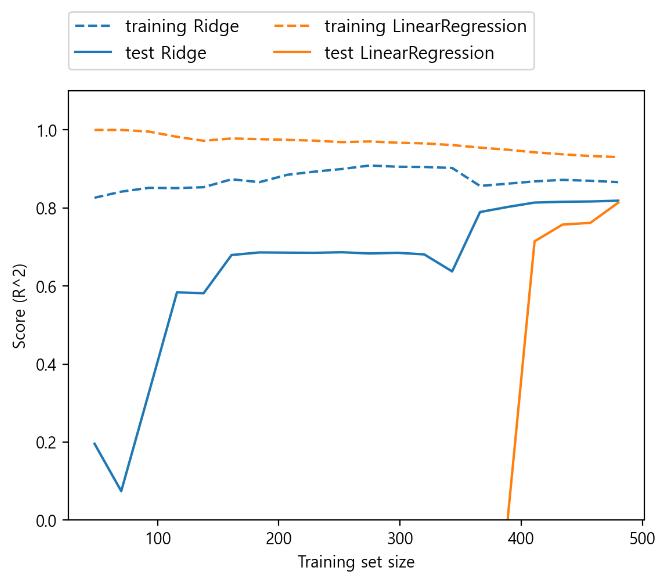
학습 곡선
데이터 셋 크기에 따른 모델의 성능 변화 그래프
- 둘다 훈련 세트의 점수가 데스트 세트의 점수 보다 높음
- 규제가 적용돤 릿지
- 훈련 데이터 점ㅎ수가 선형 회귀의 훈련 데이터 보다 점수가 맞음
- 데스트 데이터에서는 릿지 점수가 높음
- 데이터 셋이 적을 경우 차이는 더 크게 나타남
선형회귀는 데이터셋이 작을 경우 릿지보다 학습 성능이 낮음
- 데이터셋 크기가 400미만에서 어떤한 것도 학습하지 못합
- 두 모델 모두 데이터가 많을 수록 성능이 좋아짐
- 데이털가 충분하게 되면 ㄹ릿지 회귀와 선형 회귀의 성능은 같아 짐
- 상대적으로 규제 항은 덜 중요해지기 때문
라소
L1 규제의 라쏘
- 선형 회귀와 같이 계수를 적용하는 또 다른 방법
- 릿지 회귀와 같이 걔수를 0에 가깝게 해서 규제하는 방식
- 계수가 0이 되는 특성
- 모델에서 완전히 제외 됨
- 자동으로 특성이 선택된다고 볼 수 있음
- 일부 계수를 0을 만들면 이해하기 쉬워짐
- 이 모델의 가장 중요한 특성의 파악이 용이함
과소접합
from sklearn.linear_model import Lasso
lasso = Lasso().fit(X_train,y_train)
print("set score :{:.2f}".format(lasso.score(X_train,y_train)))
print("test score :{:.2f}".format(lasso.score(X_test,y_test)))
print("num :",np.sum(lasso.coef_ !=0))set score :0.29
test score :0.21
num : 4alpha 값 줄여 보기
- 과소적합을 줄이기 위한 목적
- max_intr 값 늘리기
lasso001 = Lasso(alpha=0.01,max_iter=50000).fit(X_train,y_train)
print("set score :{:.2f}".format(lasso001.score(X_train,y_train)))
print("test score :{:.2f}".format(lasso001.score(X_test,y_test)))
print("num :",np.sum(lasso001.coef_ !=0))
set score :0.90
test score :0.77
num : 33alpha 값을 너무 낮추면 규제의 효과가 없음
- 규제가 지나치게 낮으면 효과가 없어져 과대적합
lasso0001 = Lasso(alpha=0.0001,max_iter=50000).fit(X_train,y_train)
print("set score :{:.2f}".format(lasso0001.score(X_train,y_train)))
print("test score :{:.2f}".format(lasso0001.score(X_test,y_test)))
print("num :",np.sum(lasso0001.coef_ !=0))set score :0.95
test score :0.64
num : 96alpha 값이 다른 모델을의 계수
plt.plot(lasso.coef_,'^',label="Ridge alpha=1")
plt.plot(lasso001.coef_,'s',label="Ridge alpha=0.01")
plt.plot(lasso0001.coef_,'v',label="Ridge alpha=0.0001")
plt.plot(ridge.coef_,'o',label="Ridge alpha=0.1")
plt.legend(ncol=2,loc=(0,1.05))
plt.ylim(-25, 25)
plt.xlabel("계수목록")
plt.ylabel("계수크기")
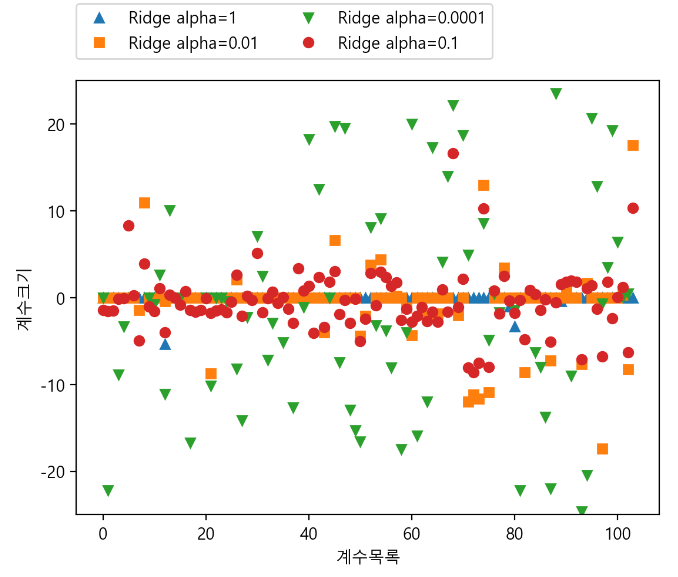
라쏘 vs 릿지
alpha = 1 : 걔수 대부분이 0, 나머지 계수들도 작음
alpha = 0.01 : 줄이면 대부분의 특성이 0이 되는 분포
alpha = 0.0001 : 계수 대부분이 0이아니고, 값도 켜져 규제없는 모델
alpha = 0.1 : Ridge모델은 alpha=0.01인 라쏘 모델과 비슷한 성능
Ridge를 사용하면 어떤 계수도 0이 되지 않음
일반적으로 라쏘보다 릿지 회귀 선호
- 특성이 많고 그 중 일부분만 중요한 경우 라쏘 사용
- 특성을 줄이고 중요한 특성을 파악할 수 있음
- 분석하기 쉬운 모델
- scikit-lean
- Lasso와 Ridge의 페널티를 결합한 ElasticNet제공
- 실제 최상의 성능 발휘
- L1 규제, L2 규제를 위한 매게변수 2개를 조정해야 함
from sklearn.linear_model import QuantileRegressor
X,y = mglearn.datasets.make_wave(n_samples=60)
X_train, X_test,y_train,y_test = train_test_split(X,y,random_state=42)
pred_up =QuantileRegressor(quantile=0.9, alpha=0.01).fit(X_train,y_train).predict(X_test)
pred_med =QuantileRegressor(quantile=0.5, alpha=0.01).fit(X_train,y_train).predict(X_test)
pred_low =QuantileRegressor(quantile=0.1, alpha=0.01).fit(X_train,y_train).predict(X_test)
plt.scatter(X_train, y_train, label="data")
plt.scatter(X_test, y_test, label="test data")
plt.plot(X_test, pred_up, label='백분위:0.9')
plt.plot(X_test, pred_med, label='백분위:0.5')
plt.plot(X_test, pred_low, label='백분위:0.1')
plt.legend()
plt.show()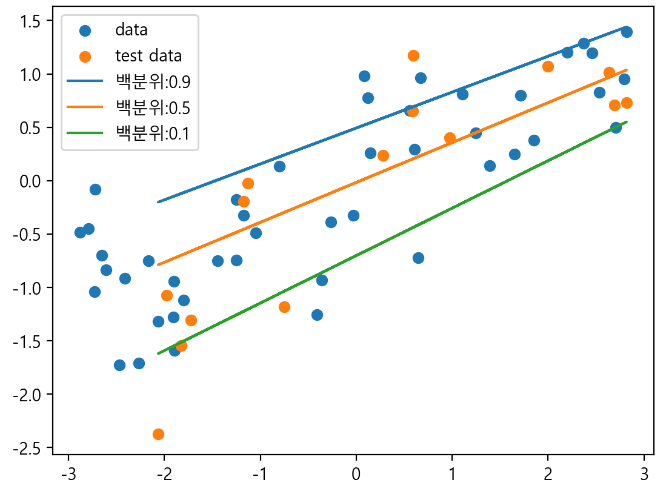
분류용 선형 모델
이진분류
- 분류에 널리 사용되는 선형모델
- 분류에 널리 사용되는 선형모델
- 선, 평면,초평면을 사용해서 두개의 클래스를 구분하는 분류기
- 이진 분류 예측방정식
- 선형 회귀와 유사
- 특성들의 합을 그냥 사용하지 않고 예측한 값을 임계치 0과 비교
- 함수에서 계산한 값
- 모든 분류용 선형모델에서 동일한 규칙
두 가지 형태의 학습 알고리즘
- 성능 측정 방법
- 특정 계수와 절편의 조합이 훈련 데이토에 얼마나 잘 맞는지 측정
- 사용 가능한 규제 방식
- 규제를 통한 과대 적합 방식
가장 널리 알려진 2개 알고리즘
- 로지스틱 회귀
- inear_model.LogisticRegressiom에 구현
- 이름에 회귀가 있지만 회귀 알고리즘이 아니라 분류알고리즘- LInearRegression 혼동 주의
- 서포트 백터 머산
- svm.LinearSVC에 구현된 선향 알고리즘
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
X,y = mglearn.datasets.make_forge()
fig, axes = plt.subplots(1, 2, figsize=(10, 3))
for model, ax in zip([LinearSVC(), LogisticRegression()], axes):
clf = model.fit(X, y)
mglearn.plots.plot_2d_separator(clf, X, fill=False, eps=0.5,
ax=ax, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y, ax=ax)
ax.set_title("{}".format(clf.__class__.__name__))
ax.set_xlabel("특성 0")
ax.set_xlabel("특성 1")
axes[0].legend()
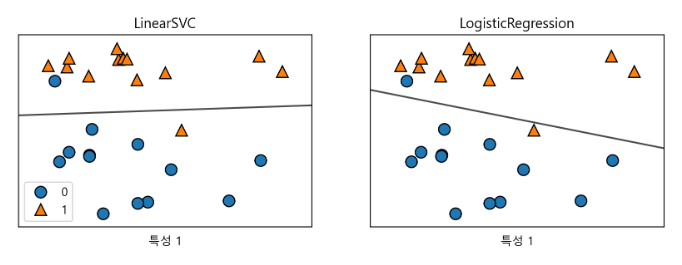
mglearn.plots.plot_linear_svc_regularization()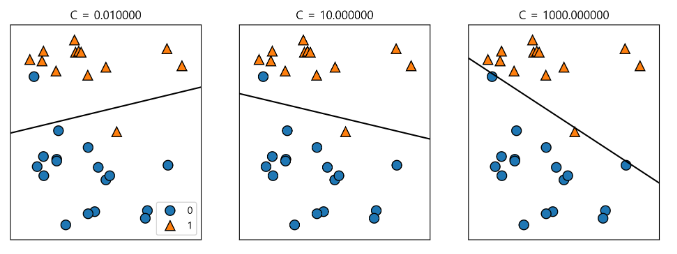
|
|
|
낮은 차원의 데이터에 대한 결정 경계
- 직선이거나 평면으로 매우 제한적이 것 처럼 보임
- 고차원에서는 매우 강력해짐
- 단, 특성이 많아지면 과대적합 되지 않도록 하는 것이 매우 중요
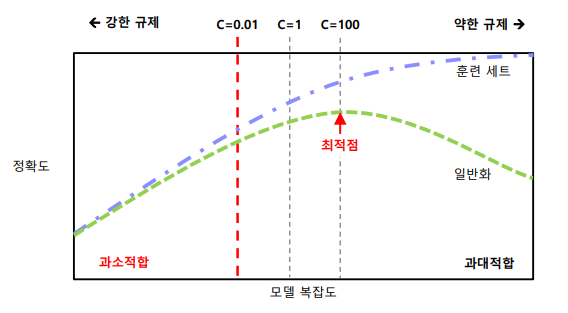
C값 규제 관계 그래프
C값이 높아지면 규제가 감소!!!! <-> 규제를 높일려면 C값 낮추기!!
높은 정확도 출력
- 기본값이 C=1이 훈련 세트와 테스트 세트 양쪽 95% 성능
- 훈련 세트와 데스트 세트의 성능이 매우 비슷함
- 제약이 너무 높아 과소적합 됨
유방암 데이터
from sklearn.datasets import load_breast_cancer
cancer = load_breast_cancer()
X_train, X_test, y_train, y_test = train_test_split(
cancer.data, cancer.target, stratify=cancer.target, random_state=42)
logreg = LogisticRegression().fit(X_train, y_train)
print("훈련 세트 점수: {:.3f}".format(logreg.score(X_train, y_train)))
print("테스트 세트 점수: {:.3f}".format(logreg.score(X_test, y_test)))훈련 세트 점수: 0.946
테스트 세트 점수: 0.965logreg100 = LogisticRegression(C=100, max_iter=5000).fit(X_train, y_train)
print("훈련 세트 점수: {:.3f}".format(logreg100.score(X_train, y_train)))
print("테스트 세트 점수: {:.3f}".format(logreg100.score(X_test, y_test)))훈련 세트 점수: 0.951
테스트 세트 점수: 0.958logreg001 = LogisticRegression(C=0.01, max_iter=5000).fit(X_train, y_train)
print("훈련 세트 점수: {:.3f}".format(logreg001.score(X_train, y_train)))
print("테스트 세트 점수: {:.3f}".format(logreg001.score(X_test, y_test)))훈련 세트 점수: 0.937
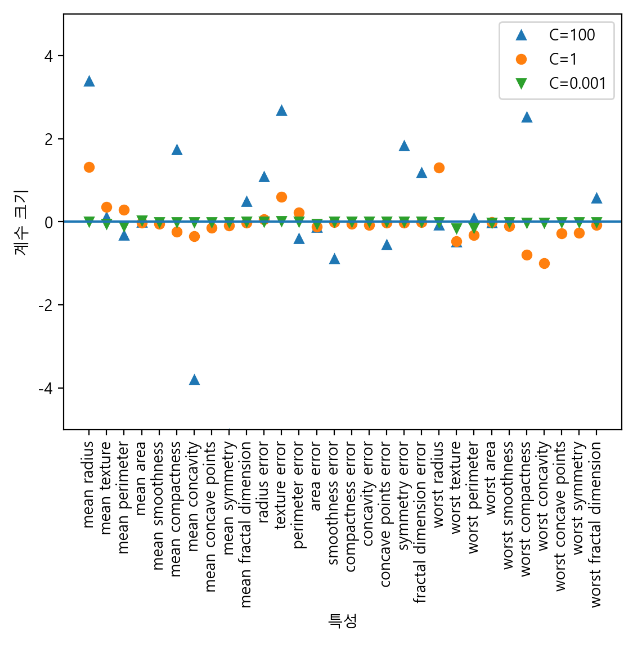
테스트 세트 점수: 0.930plt.plot(logreg100.coef_.T, '^', label="C=100")
plt.plot(logreg.coef_.T, 'o', label="C=1")
plt.plot(logreg001.coef_.T, 'v', label="C=0.001")
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
xlims = plt.xlim()
plt.hlines(0, xlims[0], xlims[1])
plt.xlim(xlims)
plt.ylim(-5, 5)
plt.xlabel("특성")
plt.ylabel("계수 크기")
plt.legend()
for C, marker in zip([0.001, 1, 100], ['o', '^', 'v']):
lr_l1 = LogisticRegression(solver='liblinear',C=C, penalty="l1",max_iter=1000).fit(X_train, y_train)
print("C={:.3f} 인 l1 로지스틱 회귀의 훈련 정확도: {:.2f}".format(
C, lr_l1.score(X_train, y_train)))
print("C={:.3f} 인 l1 로지스틱 회귀의 테스트 정확도: {:.2f}".format(
C, lr_l1.score(X_test, y_test)))
plt.plot(lr_l1.coef_.T, marker, label="C={:.3f}".format(C))
plt.xticks(range(cancer.data.shape[1]), cancer.feature_names, rotation=90)
xlims = plt.xlim()
plt.hlines(0, xlims[0], xlims[1])
plt.xlim(xlims)
plt.xlabel("특성")
plt.ylabel("계수 크기")
plt.ylim(-5, 5)
plt.legend(loc=3)C=0.001 인 l1 로지스틱 회귀의 훈련 정확도: 0.91
C=0.001 인 l1 로지스틱 회귀의 테스트 정확도: 0.92
C=1.000 인 l1 로지스틱 회귀의 훈련 정확도: 0.96
C=1.000 인 l1 로지스틱 회귀의 테스트 정확도: 0.96
C=100.000 인 l1 로지스틱 회귀의 훈련 정확도: 0.99
C=100.000 인 l1 로지스틱 회귀의 테스트 정확도: 0.98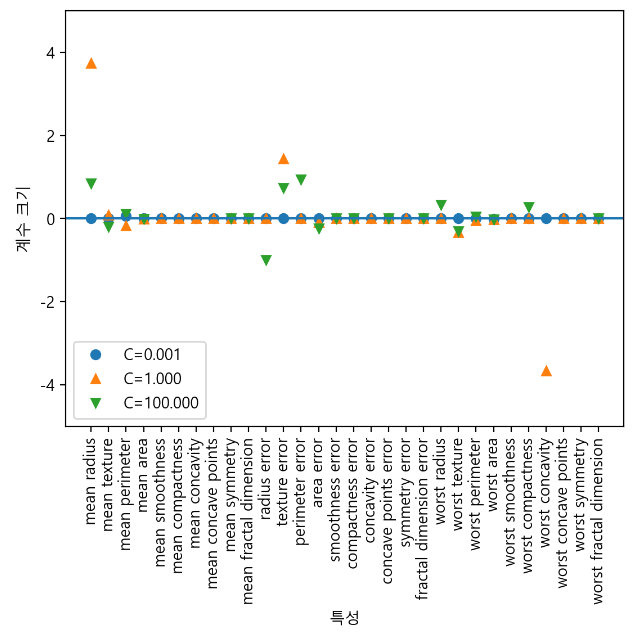
이진 분류용 선형 모델
- 회귀용 선형모델은 매우 유사함
- 모델들의 주요 처이는 규제의 설정에 따름
penalt 매개변수
- 규제에서 모든 특성을 이용하지 일부 특성을 사용할지 결정하는 매개변수
다중클래스 분류용 선형 모델
이진분류만 지원
- 로지스틱 회귀만 제외하고 선형 분류 모델은 이진 분류만 지원
- 다중 틀래스를 지원하지 않음
일대다 방식을 이용한 다중클래스 지원 가능
- 이진 분류 알고리즘을 다중 클래스 분류 알고리즘으로 확장하는 보편적 기범
- 각 클래스를 다른 모든 클래스와 구분하도록 이진 분류 모델 학습
- 클래스의 수 만큼 이진 분류 모델 생성
- 예측 시에는 모든 이진 분류기가 작동
- 가장 높은 점수를 내는 분류기의 클래스 선택하는 방식
클래스별 이빈 분류기의 생성
- 각 클래스가 계수 벡터(w)와 절편(b)를 하나씩 가짐
- 분류 신로도를 나타내는 다음 공식의 결과 값
- 가장 높은 클래스가 해당 데이터의 클래스 레이블로 할당
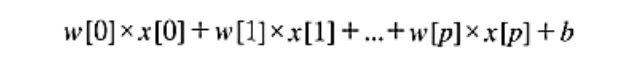
다중 클래스 로지스택 회귀
- 일대다 방식과 다른 수학 방식 사용
- 동일하게 클래스 마다 하나의 걔수 벡터와 절편 생성
- 동일한 예측 방식
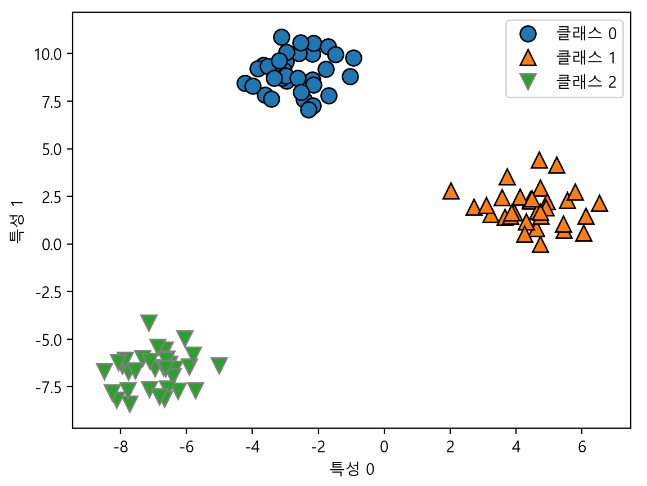
세 개의 클래스를 가진 간단한 데이터 셋에 일대다 방식 적용하기
- 2차원 데이터 셋
- 각 클래스의 데이터는 정규분포(가우시안 분포)를 따름
from sklearn.datasets import make_blobs
X, y = make_blobs(random_state=42)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
plt.legend(["클래스 0", "클래스 1", "클래스 2"])
linear_svm = LinearSVC().fit(X, y)
print("계수 배열의 크기: ", linear_svm.coef_.shape)
print("절편 배열의 크기: ", linear_svm.intercept_.shape)계수 배열의 크기: (3, 2)
절편 배열의 크기: (3,)mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.ylim(-10, 15)
plt.xlim(-10, 8)
plt.xlabel("특성 0")
plt.ylabel("특성 1")
plt.legend(['클래스 0', '클래스 1', '클래스 2', '클래스 0 경계', '클래스 1 경계',
'클래스 2 경계'], loc=(1.01, 0.3))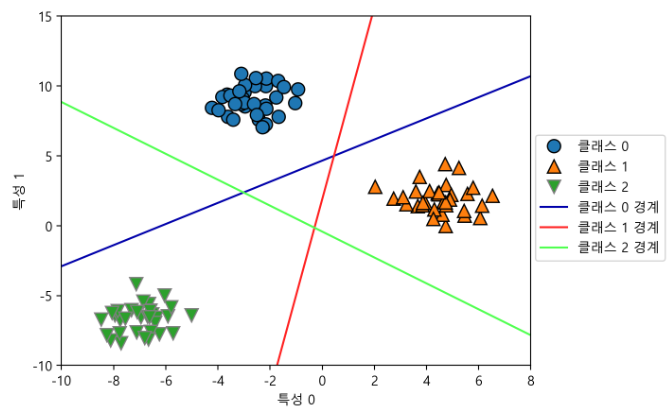
실행결과 분석 )
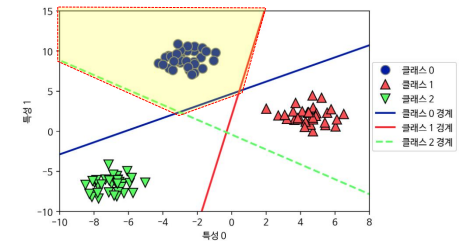
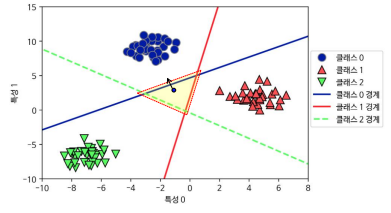
실행결과 분석1 / 2
|
훈련 데이터의 클래스 0의 모든 포인트
|
중앙의 삼각형 영역
|
mglearn.plots.plot_2d_classification(linear_svm, X, fill=True, alpha=.7)
mglearn.discrete_scatter(X[:, 0], X[:, 1], y)
line = np.linspace(-15, 15)
for coef, intercept, color in zip(linear_svm.coef_, linear_svm.intercept_,
mglearn.cm3.colors):
plt.plot(line, -(line * coef[0] + intercept) / coef[1], c=color)
plt.legend(['클래스 0', '클래스 1', '클래스 2', '클래스 0 경계', '클래스 1 경계',
'클래스 2 경계'], loc=(1.01, 0.3))
plt.xlabel("특성 0")
plt.ylabel("특성 1")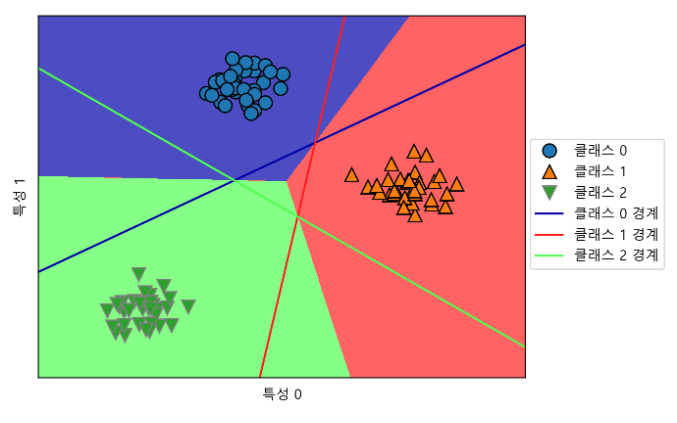
3개의 일대다 분류기가 만든 다중 클래스 결정 경계
- 공동 구역에 있는 포인트는 가까운 직선의 분류에 포함
- 영역이 3개 클래스에 맞게 분류됨
선형 모델의 주요 매개변수
- 회귀 모델의 주요 매개변수
- alpha값이 클수록 단순화
- alpha 값을 조정하는 일이 매우 중요
- LinearSVC와 LInearRegression에서는 c
- c값이 작을 수록 단순화
- c와 alpha의 최적치 정하기
- 보통 로그 스케일로 최적치 산출
- 이후 L1 규제를 사용할지 L2 규제를 사용할지 결정
- 기본적으로 l2규제 사용
- L1 규제는 모델의 해석이 중요한 요소일 때도 사용 가능
- 몇 가지 특성만으로 사용하므로 중요한 특성 파악 및 효과 이해 용이
빠른 학습 속도와 예측 속도
- 매우 큰 테이터셋과 희소한 데이터셋에서도 잘 작동
- 수십마에서 수백만개으 샘플로 이루어진 대용량 데이터셋
- LInearRegression과 Ridge에 solver='sag' 옵션 사용하는 방법
- 기본 설정 보다 빨리 처리 가능
- 대용량 처리 버전의 선형 모델 사용하는 방법
- SDGClassifier
- SDGRegressor
- LInearRegression과 Ridge에 solver='sag' 옵션 사용하는 방법
선형 모델의 장 단점
- 공식을 사용해 예측 과정을 비교적 쉽게 이해
- 하지만 개수의 값들에 대해 이해할기 어려우 수 있음
- 데이터 셋의 특성들 간에 연관이 있으 경우 분석의 어려움
- 샘플에 비해 특성이 많을 때 적합한 모델
- 다른 모델로 학습하기 어려운 매우 큰 데이터셋에도 선형 모델 다수 사용
- 저차원의 데이터셋은 다른 모델의 일반화 성능이 더 좋음

#ABC부트캠프 #부트캠프 #유클리드소프트 #파이썬 #고용노동부 #한국산업인력공단 #청년친화형 #ESG지원사업 #대전 #서포터즈 #python #Ai #Bigdata #cloud #대외활동 #대학생 #daily